
Investigación
Formación estadística de estudiantes para profesor en matemática: un estudio exploratorio
Statistical training of students for teacher in Mathematics: an exploratory study
Claudia Noemí Ferrari* Ana Rosa Corica**
* Maestra en Estadística Aplicada, Profesor Titular, Facultad de Ciencias Económicas, Universidad Nacional de La Plata, Argentina, claudianferrari@yahoo.com.ar
** Doctora en Ciencias de la Educación, Investigador Adjunto, Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Profesor Adjunto, Universidad Nacional del Centro de la Provincia de Buenos Aires, Argentina, acorica@exa.unicen.edu.ar
Recibido: 14 de julio de 2017
Aceptado: 05 de diciembre de 2017
Resumen
Este trabajo se ubica en la formación estadística de estudiantes para profesor en matemática. Con fundamento en la Teoría Antropológica de lo Didáctico, reportamos resultados del diseño, validación y aplicación de un cuestionario. Éste tiene como propósito caracterizar las praxeologías en torno a la estadística que los estudiantes de profesorado hacen explícitas al resolver tareas esenciales del área. Los resultados serán empleados en investigaciones futuras con el propósito de modificar las praxeologías matemáticas actuales en estadística en la formación de profesores. El cuestionario se implementó en seis instituciones no universitarias y se compone de tareas en las que priorizamos la interpretación y el análisis de información por sobre el cálculo rutinario, dado que éste se desvanece con el tiempo. La información relevada puso de manifiesto dificultades de los estudiantes en el hacer de las tareas. Inferimos que éstos identifican el entorno tecnológico demandado para resolver la tarea con la aplicación de fórmulas.
Palabras clave: Formación de profesores; estadística; conocimiento matemático; encuestas.
Abstract
This work is set in the problematic of the statistic formation of mathematics trainees. With basis in the Anthropological Theory of the Didactical, we report the results of the design, validation and application of a survey. This instrument is proposed to characterise the praxeology about statistic that the mathematics trainees make explicit when solving essential tasks of the area. The results will be used in future research with the purpose of modifying current mathematical praxeologies of statistics in teacher training. The survey was implemented in 6 tertiary institutions non – university. In the survey we prioritized the interpretation and analysis of information on routine calculation because the latter fades with time. The information collection revealed difficulties in solving the proposed tasks. We infer that the mathematics trainees identify the technological environment required to solve of the task with the application of formula.
Keywords: Mathematics trainees; statistics; mathematical knowledge; surveys.
Introducción
La sociedad actual se encuentra regida por la información, y para el desempeño competente del ciudadano se requiere de una formación que le permita analizar e interpretar dicha información y los datos que se producen. Del Pino y Estrella (2012) señalan que "estamos inmersos en ingentes cantidades de datos con los que nos invaden los medios de comunicación en la forma de tablas y gráficos, y es necesario ser capaces de comprender y usar esta información" (p. 54). Por esta razón, el ciudadano debe tener una actitud crítica ante los argumentos estadísticos que se esgrimen. Los sistemas de enseñanza de secundaria tienen un rol preponderante en la formación de los ciudadanos, sin embargo, el curriculum de matemática resulta obsoleto; se requiere de una renovación urgente de dicho curriculum donde la estadística ocupe un lugar esencial (Chevallard, 2017).
El reconocimiento del papel fundamental de la estadística en el desarrollo de la sociedad moderna, ha llevado al abordaje de su estudio en la formación básica. En el caso de incluir nociones estadísticas en las aulas, se tiende a enfocar su instrucción en los aspectos más procedimentales vinculados al cálculo, con énfasis operacional y no en la comprensión conceptual o aspectos interpretativos, sin percibir que es una herramienta indispensable para la vida académica y profesional del ciudadano de hoy (Batanero, Gea, López-Martín & Arteaga, 2017; Estrada, 2002; Estrada, Batanero & Fortuny, 2006; Watson, 2001).
Una de las razones fundamentales por las que se encuentra ausente el estudio de la estadística en la escuela secundaria, se vincula al hecho de que los profesores "se enfrentan ante una propuesta externa para la incorporación de este nuevo conocimiento que en la mayoría de los casos no conocen" (Azcárate, 2006, p. 8). En particular, Arteaga, Batanero, Cañadas y Gea (2012) indican que "algunos profesores de matemáticas se encuentran inseguros al enseñar esta materia" (p. 280).
Diversas investigaciones ponen en evidencia la deficitaria comprensión de los conocimientos estadísticos que poseen tanto los profesores en formación como en actividad, producto de la preparación insuficiente (Azcárate, 1996; Azcárate & Cardeñoso, 2011; Cardeñoso, 2001; Carnel, 1997; Estrada, 2011; Estrada, Batanero & Fortuny, 2004; Serradó, Azcárate & Cardeñoso, 2005, 2006; Moreno, Cardeñoso & González García, 2012). Investigaciones como las de Araneda, del Pino, Estrella, Icaza y San Martín (2011), Ben-Zvi y Sharett-Amir (2005), Garfield y Ben-Zvi (2007), del Pino y Estrella (2012), indican que los profesores confunden los propósitos de la enseñanza de la estadística, porque los identifican con el aprendizaje de reglas para calcular medidas de tendencia y técnicas para representar datos por medio de tablas y gráficos. Por este motivo, la enseñanza de la estadística en la escuela secundaria requiere de una modificación en la formación de los docentes.
Según Godino, Giacomone, Batanero y Font (2017), "el profesor de matemáticas tiene que conocer las matemáticas escolares del nivel educativo donde imparte, pero también debe poder articular esos conocimientos con los correspondientes a algunos niveles posteriores" (p. 96). Siguiendo esta perspectiva, en este trabajo nos proponemos indagar la formación en estadística de estudiantes para profesor de matemática de la escuela secundaria, con el propósito de emplear estos resultados para modificar las praxeologías matemáticas en torno a la estadística que se estudian en la formación docente.
Con fundamento en la Teoría Antropológica de lo Didáctico, proponemos un estudio que involucra a estudiantes que realizan sus estudios en instituciones terciarias no universitarias en Argentina. Estos estudiantes pertenecen a seis institutos de formación docente de una región distrital de Argentina, siendo las únicas instituciones donde pueden realizar estos estudios. Ellos son quienes se ocuparán fundamentalmente de la educación en matemática de la escuela secundaria de la región. Reportamos resultados del diseño, validación y aplicación de un cuestionario que permitió caracterizar los elementos de las praxeologías en torno a la estadística, que estudiantes para profesor en matemática hacen explícitos al resolver tareas esenciales del área.
1. Marco Teórico
En este trabajo adaptamos como marco teórico la Teoría Antropológica de lo Didáctico (TAD) (Chevallard, 1999). El postulado base de la TAD supone que toda actividad humana regularmente realizada se puede describir mediante un modelo denominado praxeología (Chevallard, 1999). El concepto de praxeológica u organización matemática (OM), se comprende a partir de sus elementos constitutivos. El corazón de la noción de praxeología lo constituye la tarea, t, y el tipo de tareas, T, a la que pertenece. Calcular la mediana de un conjunto de datos, puede servir como ejemplo de tarea, en tanto que simplemente Calcular, es un género de tarea (G). Tanto las tareas t como los tipos T y géneros de tarea G, son construcciones institucionales cuya reconstrucción, en una institución determinada, es el objeto mismo de la didáctica (Chevallard, 1999). La manera de realizar una tarea se denomina técnica τ; ésta no necesariamente es única y depende de la institución en que se realiza el estudio. Por ejemplo, al calcular la mediana de un conjunto de datos, se puede hacer mediante un algoritmo o bien obtener su valor desde la representación gráfica de los datos. El discurso racional que permite justificar y explicar a la técnica τ, empleada al realizar el tipo de tareas T, se denomina tecnología θ. Esta tecnología tiene, como función además, aportar elementos para desarrollar la técnica, con la finalidad de ampliar su alcance, superar sus limitaciones y hacer posible la producción de nuevas técnicas. El último nivel de justificación de la actividad matemática lo constituye la teoría Θ (asociada a una tecnología) y resulta ser la tecnología de esta tecnología.
Los elementos de una OM se estructuran en dos niveles interrelacionados entre sí. Uno de ellos es el nivel de la praxis, formado por las tareas problemáticas y las técnicas requeridas para resolverlas. El otro es el nivel del logos, que contempla la tecnología y la teoría que se necesitan para la praxis. Las componentes de una OM se encuentran fuertemente relacionadas entre sí. Al desarrollar una técnica, se generan nuevos tipos de tareas y se requieren nuevas explicaciones y justificaciones. Así, aparecen nuevas OM que amplían y completan las anteriores. En la TAD se propone clasificar las OM según las características de sus componentes. Se comprende a una OM como puntual (OMP) en una determinada institución, cuando es generada por un único tipo de tareas T. La integración de diversas OMP en torno a un discurso tecnológico θ común en una institución, genera una praxeología local (OML). Esta integración puede dar respuesta a un conjunto de cuestiones problemáticas que no pueden ser resueltas en su totalidad por ninguna de las OMP iniciales. Mientras que una praxeología se denomina regional (OMR) en una institución, si es obtenida a partir de la coordinación, articulación e integración de diversas OML, en torno a una teoría común Θ (Bosch, Fonseca & Gascón, 2004). Por último, las OM Globales (OMG) son producto de la agregación de OMR (Chevallard, 1999).
Fonseca (2004) establece las características que deben poseer las OM, para poder integrarse en una OML, siendo que los sistemas de enseñanza deberían, al menos, procurar reconstruir una OML. El cumplimiento de estas características da cuenta de cierto grado de completitud de las OM. En el proceso de estudio de una OML relativamente completa se distinguen dos partes, una relativa al proceso de construcción o reconstrucción de la propia OM determinada por los Momentos Didácticos, y otra, relativa al propio producto resultante. En particular, en lo que concierne al estudio del producto del proceso de construcción, se realiza en relación con los siguientes indicadores establecidos originalmente por Fonseca (2004) y ampliado por Lucas (2010):
En correspondencia con lo establecido por los indicadores, el estudio de la matemática requiere de la manipulación de diversas técnicas y es posible comprender la funcionalidad de las mismas en el estudio de distintas situaciones. Esto permite analizar y establecer los alcances y limitaciones al emplear una técnica u otra.
Algunos de los indicadores mencionados fueron tomados como base para poder confeccionar el cuestionario que se involucra en esta investigación.
2. Metodología
El diseño de investigación propuesto es el estudio de caso (Skate, 1999). Se trata de una investigación de naturaleza descriptiva, exploratoria e interpretativa. Se propone caracterizar el hacer de un conjunto de tareas prototípicas en torno a la estadística, según la formación propuesta a estudiantes para profesor en matemática, a partir de la aplicación de un cuestionario diseñado ad hoc (en adelante, CTE: Cuestionario de Tareas Estadísticas). El estudio se desarrolló con estudiantes para profesor en matemática (EPM), que se encontraban cursando el último año de la carrera en instituciones terciarias no universitarias, que en Argentina son denominadas Institutos Superiores de Formación Docente (ISFD). En estas instituciones, la carrera Profesorado en Matemática para la enseñanza secundaria tiene una duración de cuatro años y el plan de estudios se rige por el Diseño Curricular (1999), común a todas estas instituciones de una misma provincia. Los 69 ISFD que ofrecen la carrera de interés en la provincia de Buenos Aires se encuentran distribuidos en 25 unidades espaciales delimitadas, de acuerdo con un programa de acción, las que son denominadas Regiones Educativas (RE). Se generó una muestra por conveniencia de caso-típico, pues "el objetivo es la riqueza, profundidad y calidad de la información, no la cantidad ni la estandarización" (Hernández, Fernández & Baptista, 2010, p. 397).
Los ISFD que integraron los puntos muestrales son aquellos emplazados en la región 4 (RE 4) conformada por los partidos de Quilmes, Berazategui y Florencio Varela, en los que hay tres ISFD de gestión estatal y tres de gestión privada. En estos institutos, la estructura curricular de la carrera se encuentra plasmada en el Diseño Curricular Provincial (1999) para la formación docente, e incluye diferentes espacios compuestos por grupos de materias anuales. En particular, el Espacio de la Orientación se conforma por 18 materias y contempla el estudio de Probabilidad y Estadística en el 3° año, con un total de tres horas semanales.
El CTE fue aplicado personalmente a los estudiantes de los seis ISFD en su horario habitual de clase y en presencia del profesor que en ese momento se encontraba a cargo de la clase de 4° año. Esto es para garantizar que los participantes de este estudio recibieron la capacitación básica que les permite tener ideas formadas sobre las cuestiones que se indagan en el CTE. La aplicación del instrumento tuvo lugar luego de seis meses de iniciado el ciclo lectivo 2016. El tiempo que demandó la aplicación del CTE en cada ISFD, fue aproximadamente una hora. Con la intención de preservar el anonimato de los estudiantes, se asignó un código a cada uno de los CTE.
2.1 El cuestionario
Para el diseño del CTE, se consideraron las nociones estadísticas establecidas en el Diseño Curricular, presentes en los materiales de estudio editados por quienes tienen a cargo la formación estadística de los EPM que participaron de la investigación. También se atendieron a los resultados de investigaciones sobre la educación estadística de profesores de matemática en ejercicio y en formación (Burrill & Biehler, 2011 citado en Batanero, 2013, p. 3).
Finalmente, los ítems del CTE involucraron temáticas asociadas al relevamiento de información, a las representaciones gráficas de datos, a las medidas de tendencia central y de variabilidad, y a correlación y regresión lineal. Una vez seleccionadas las nociones estadísticas, se consideraron los indicadores de completitud de OML propuestos por Fonseca (2004) y Lucas (2010) para la redacción de las tareas del CTE. En esta construcción se excepcionaron los indicadores OML7 y OML8. La presencia o ausencia de estos indicadores requiere de un proceso de estudio que no puede limitarse a un espacio temporal como demanda el cuestionario que proponemos.
Una versión piloto del CTE fue sometida a juicio de ocho expertos con la intención de determinar la validez del contenido del cuestionario. Los resultados se cuantificaron mediante el cálculo de un índice de concordancia entre jueces, denominado coeficiente de validez V de Aiken (Aiken, 1980). Un espacio destinado a Observaciones permitió recoger cualquier comentario que los jueces pudieran realizar en torno a cada ítem y/o a su evaluación. La valoración de los jueces aportó comentarios que permitieron reformular la presentación de algunas tareas originales. Con los resultados de la evaluación se construyó la versión definitiva del CTE. Ésta contempla seis ítems que incluyen 14 tareas. También fue incorporado al instrumento un ítem abierto denominado Observaciones, de modo que los estudiantes pudieran registrar todo comentario relacionado a las tareas estadísticas propuestas.
2.1.1 Caracterización de las tareas del cuestionario
Las tareas del CTE pertenecen a los ocho géneros de tareas que se describen a continuación y que se consideran fundamentales en el estudio de las nociones estadísticas:
A continuación describimos cada uno de los ítems que componen el CTE. Indicamos el género al que pertenecen y el indicador matemático de completitud de OML al que refiere directamente su hacer.
El ítem 1 (Tabla 1) refiere a medidas de posición y dispersión. Estas tareas pertenecen a los géneros de tarea G7 y G6. La inclusión de este ítem tuvo en cuenta que las medidas de tendencia central son la base para la comprensión de muchas otras nociones estadísticas.

Uno de los conceptos que más interés ha suscitado, dentro de la investigación en educación estadística son los promedios, sobre cuya comprensión y cálculo se han realizado diversas investigaciones que describen errores y concepciones erróneas en estudiantes de diversas edades, particularmente en alumnos universitarios. (Cobo, 2003, p. 8)
Además, razonar mediante nociones estadísticas y dar sentido a la información estadística, depende de la comprensión de un concepto clave como es el de variación (Garfield, 2002; Moore, 1990; Wild & Pfannkuch, 1999).
En el ítem 1, la propuesta de un valor para la media aritmética superior al valor del tercer cuartil (Tabla 1, inciso a), pretende que el entorno tecnológico contemple las definiciones de dichas nociones estadísticas y la influencia que pudiera tener, o no, sobre ellas la presencia de datos atípicos. El entorno tecnológico para el inciso b) (Tabla 1), contempla además la definición de varianza, como indicador de la variación de los datos en torno a la media aritmética. Dado que los valores de las medidas de posición y dispersión fueron suministrados, no se requiere técnicas para su cálculo. Asociamos el ítem 1 (Tabla 1) a los indicadores de completitud OML1, OML5.
La tarea del ítem 2 (Tabla 2) refiere al estudio de correlación y regresión lineal. El estudio de estas nociones involucra procesos iniciales de inferencia estadística, permitiendo hacer estimaciones en contextos donde el azar se encuentra presente. La tarea refiere a una posible relación lineal entre pares de variables numéricas continuas. Esta tarea pertenece a los géneros de tarea G4, G2, G3 y G6. El entorno tecnológico que justifica el hacer de la tarea involucra las nociones de diagrama de dispersión, coeficiente de correlación lineal y recta de regresión lineal.
Para Estepa (2008) "el diagrama de dispersión es la herramienta gráfica más usada, sencilla y potente para analizar la relación que puede existir entre dos variables" (p. 258). Al confeccionar los posibles diagramas de dispersión, la observación de la nube de puntos más concentrada en torno a la recta de regresión será suficiente para tomar la decisión. Otra técnica complementaria y analítica consiste en la determinación del coeficiente de correlación lineal. La existencia de diferentes técnicas para poder abordar el ítem da cuenta del indicador de completitud OML2. Además, el hacer de este ítem se encuentra asociado al indicador OML1.
Las tareas que involucra el ítem 3 (Tabla 3) refieren al estudio de datos de una variable numérica continua, Salario, expresada en salarios mínimos. Estas tareas pertenecen a los géneros de tarea G2, G3, G4 y G5. El entorno tecnológico que justifica el hacer del inciso 3a) (Tabla 3) contempla las definiciones de frecuencia absoluta, la construcción de diferentes gráficos para representar variables numéricas continuas, como las definiciones de medidas de posición y dispersión. La descripción de la distribución de la variable Salario puede requerir de la representación gráfica de los datos. El lenguaje gráfico tiene un papel esencial en la organización, descripción y análisis de datos (Wild & Pfannkuch, 1999). Para Gal (2002), la construcción e interpretación de gráficos estadísticos es parte importante de la cultura estadística.
Tabla 3. Tercera tarea del cuestionarioresultados de investigación
La construcción del histograma demanda organizar la información en una tabla de frecuencias para datos agrupados, atendiendo al tipo de variable y la cantidad de datos. A partir del gráfico, la descripción de la distribución de la variable requiere de la identificación del valor central, el máximo y el mínimo, la simetría de la gráfica y la presencia de valores alejados; es decir, se describe su centro, su forma y dispersión.
Otra técnica analítica consiste en calcular las medidas resumen; algunas de ellas estarán vinculadas al centro (media aritmética, mediana o moda); otras, asociadas a la dispersión (rango, desvío estándar, valores atípicos), y también medidas que den cuenta de la forma de la distribución (coeficiente de asimetría).
La tarea del inciso 3b) (Tabla 3) se asocia al género G6. La tarea requiere de la organización de los datos de la variable Salario en dos tablas de frecuencias, asociadas a la región de procedencia de los docentes (interior o capital). El hacer de esta tarea admite el empleo de una técnica gráfica mediante la construcción de dos histogramas o gráficos de caja (uno para los salarios de docentes del interior y otro para los salarios de docentes de la capital). De esta manera, se podrá comparar la forma, centro y dispersión. Otra técnica complementaria y analítica emplea los valores de medidas resumen, calculados a partir de las tablas de frecuencia.
Las tareas del inciso 3c) (Tabla 3) pertenecen a los géneros de tarea G3, G7 y G8. El hacer de estas tareas requiere de un entorno tecnológico que contemple, además de las nociones de medidas resumen, las propiedades algebraicas que satisfacen las operaciones entre números reales. Una técnica elemental para poder realizar la tarea, radica en generar nuevos datos: para el inciso i) se puede sumar a cada dato original, el 35%, o bien, multiplicar cada uno de ellos por 1,35. Para el inciso ii) se puede sumar a cada valor la constante real 1. De esta forma, a partir de los datos originales y de los nuevos, se puede interpretar la incidencia sobre estas medidas de las transformaciones. Una técnica algebraica y general se basa en la utilización de fórmulas para el cálculo de las medidas resumen y en propiedades algebraicas, comparando las expresiones de la media, mediana y desvío estándar para datos xi, con las respectivas para datos de la forma cxi, siendo c una constante real, y con aquellos de la forma xi + c, siendo c una constante real. Debido a la existencia de diferentes técnicas (aritméticas, gráficas y algebraicas) que admite el hacer del ítem 3 (Tabla 3), éste da cuenta de los indicadores de completitud OML1 y OML2.
En el ítem 4 (Tabla 4) se presenta el gráfico de caja para los datos de la variable numérica continua Edad, presentados en la tabla del ítem 3 (Tabla 3). En este ítem se intenta revertir la típica tarea de cálculo de los cinco números resumen y la posterior construcción de un gráfico de caja. Aquí no se requiere ni el cálculo de medidas descriptivas, ni la construcción de gráficos. De este modo, el hacer del ítem se vincula con el indicador de completitud OML4.
La tarea que involucra el inciso 4a) (Tabla 4) se relaciona con los géneros de tarea G5 y G7. El entorno tecnológico que involucra el hacer de la tarea contempla las nociones de diagrama de caja; propiedades de robustez de las medidas de centralización, y la noción de simetría junto con el cálculo del coeficiente de asimetría. La inspección del gráfico de caja muestra que la media aritmética y la mediana coinciden. Dado que los datos de la variable Edad fueron provistos con anterioridad, otra técnica analítica consiste en calcular el coeficiente de asimetría. El indicador de completitud que se vincula con esta tarea es OML2.
Las tareas de los incisos 4b) y 4c) (Tabla 4) se vinculan con el género de tarea G7. Para las tareas de ambos incisos es necesario interpretar en el gráfico de caja el percentil de 5% y el percentil de 95%. El entorno tecnológico incluye tanto la noción de percentil como la construcción de un gráfico de caja. Complementariamente, se pueden calcular estos estadísticos de posición a partir de los datos presentados en la tabla del ítem 3 (Tabla 3). El indicador del grado de completitud que se vincula con el hacer de esta tarea es OML2.
En las tareas del ítem 5 (Tabla 5) es necesario indicar el valor de verdad de las cuatro proposiciones que refieren a medidas descriptivas de la variable numérica discreta Cantidad de hijos. Se presenta un gráfico de barras y una tabla que contiene las medidas descriptivas obtenidas con un software estadístico. Las tareas del ítem 5 (Tabla 5) se corresponden con el género de tarea G7. El entorno tecnológico contempla las nociones de asimetría de una distribución y el criterio del coeficiente de asimetría. La lectura del gráfico de barras permite detectar su asimetría respecto del valor central. Además, esa asimetría se pone en evidencia a partir del coeficiente de asimetría que se presenta en la tabla de estadísticos. Los indicadores de completitud asociados a esta tarea son OML1 y OML2.
El hacer de la tarea 5b) (Tabla 5) demanda observar el gráfico de barras y determinar el valor de la variable que presenta la barra de mayor longitud. El entorno tecnológico contempla las nociones de frecuencia absoluta y moda para una variable numérica discreta y la construcción de gráficos de barras.
En el hacer de la tarea 5c) (Tabla 5), al analizar el gráfico de barras se puede observar que de los 20 profesores casados, tres tienen tres hijos; esto se determina por la altura de la barra sobre el valor tres de la variable considerada. El entorno tecnológico de este inciso contempla las nociones de frecuencia absoluta, frecuencia relativa y percentil. Esta última noción se requiere a efectos de no confundir la información que presenta la tabla de estadísticos, en la que se indica que a P(95) le corresponde el valor 3.
En el hacer del tipo de tarea que involucra el inciso 5d) (Tabla 5), el entorno tecnológico contempla las nociones de cuartil, rango intercuartílico y valor atípico. La afirmación puede justificarse a partir de la tabla de estadísticos, determinándose el valor de 3 +1.5 RI (4,5) que delimita a los datos atípicos. Otra técnica alternativa consiste en comparar el dato 5 con el valor P(95). De esta forma, la diversidad de técnicas para dar respuesta a las tareas de este ítem y la interpretación de resultados, permite indagar el cumplimiento del indicador de completitud OML1 y OML5.
Las tareas del ítem 6 (Tabla 6) indagan el cumplimiento del indicador de completitud existencia de tareas matemáticas "abiertas" (OML6). Estas tareas intentan revertir las situaciones típicas de suministrar datos de alguna variable estadística, prescindiendo del modo de relevamiento de la información. Este ítem se vincula con los géneros de tarea G1, G4 y G5, y demandan reconocer, entre la información disponible en el celular, aquella que puede considerarse una variable estadística. El modo en que se presenten los datos incluye la construcción de una tabla de frecuencias. Una técnica gráfica de presentación de la información demanda construir un gráfico que muestre las características de la información registrada, la que también se puede presentar mostrando las medidas resumen adecuadas. El entorno tecnológico de este ítem, contempla las nociones de variable estadística y su clasificación, de frecuencia absoluta y relativa, de gráficos estadísticos y de medidas resumen. De esta forma, la tarea permite indagar el cumplimiento del indicador de completitud OML5.

3. Resultados
La implementación del CTE permitió obtener una muestra de n = 38 cuestionarios. Destacamos que 22 participantes se forman en ISFD de gestión pública y los 16 restantes lo hacen en instituciones de gestión privada.
Para realizar la descripción de las respuestas de los EPM a cada ítem, se decidió agrupar las mismas definiendo un conjunto de categorías, como sigue:
Con estas categorías de respuesta se estudió la consistencia interna del CTE mediante el coeficiente alfa de Cronbach, que permite estimar la fiabilidad de un instrumento, asumiendo que los ítems miden un mismo constructo y están altamente correlacionados (Welch & Comer, 1988). La determinación del alfa se realizó con el software SPSS 15.0. Se obtuvo valor alfa = 0,91, superando el "valor mínimo aceptable de 0,7" (Celina & Campo, 2005, p. 577).
Para cada una de las tareas del CTE, se computó la frecuencia de las diferentes categorías de respuesta. En la Tabla 7 se presentan los valores obtenidos.
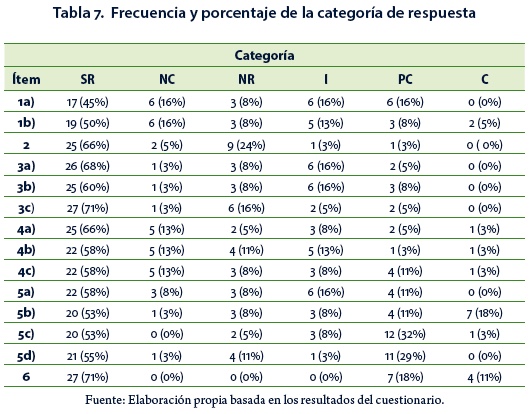
En el inciso 1a) (Tabla 1), se destaca un alto porcentaje de estudiantes que no dio respuesta a la tarea (45% en SR). Además, 16% de los EPM manifiesta desconocer el entorno tecnológico-teórico necesario para el hacer de la tarea. En particular, las producciones registradas que se corresponden con la categoría PC, contienen la respuesta correcta, pero el entorno tecnológico que la justifica, no es el adecuado. Una respuesta prototípica de esta categoría señala que "menos de 50 alumnos, porque el 75% son 50 alumnos" (Protocolo DE2-GE-06). El porcentaje al que alude el EPM permite inferir que, por una parte, confunde la variable en estudio (cantidad de alumnos por curso), con la totalidad de estudiantes en la Universidad y, por otra, se observa la inapropiada interpretación del tercer cuartil.
Las respuestas pertenecientes a la categoría I muestran el desconocimiento del entorno tecnológico-teórico requerido: la falta de robustez de la media aritmética ante valores atípicos. Se destaca que este ítem no fue respondido correctamente por ninguno de los participantes.
Con relación al ítem 1b), el 50% de los protocolos pertenece a la categoría SR (Tabla 7). En el resto de los protocolos, se destacan aquellas respuestas que aluden a un entorno tecnológico constituido por fórmulas, tal como indica el siguiente estudiante: "Recuerdo que en el curso de Probabilidad y Estadística vimos este tipo de ejercicio, pero no recuerdo su resolución con exactitud, sé que usábamos fórmulas para poder calcularlo pero no las recuerdo" (Protocolo DE1-GE-05). Esto nos conduce a concluir que hay una inadecuada interpretación de la tarea por parte de los estudiantes, dado que ningún cálculo es requerido.
En el ítem 2 (Tabla 2), no se registraron respuestas correctas. Sólo se obtuvo una respuesta de la categoría I y una de la categoría PC (Tabla 7). Se destaca que ninguna de las respuestas contiene la representación gráfica, a pesar de que el enunciado del ítem lo solicita.
En el ítem 3a) (Tabla 3) se registró que 68% de los cuestionarios no fue respondido (SR). La categoría PC representa 5% de las respuestas (Tabla 7). En este caso, sólo dos participantes especifican el valor máximo de la variable Salario, y de ellos, uno señala el valor mínimo. Una respuesta prototípica de la categoría I señala que "La característica más relevante es que los datos del salario están ordenados de forma ascendente" (Protocolo DE1-GE-05). Aquí se observa una interpretación débil de la información brindada. Se manifiesta confusión entre la presentación de los datos y la distribución de la variable de la que provienen.
Destacamos que en ningún protocolo se propone la construcción de una tabla de frecuencias, ni la representación gráfica de los datos o el cálculo de alguna medida resumen. Sin el empleo de algunas de estas técnicas, resulta difícil describir la distribución de una variable y resumirla con alguna medida adecuada.
La ausencia de las técnicas antes descritas se replica en el hacer de la tarea del inciso 3b) (Tabla 3). Aquí, la categoría I reúne 16% de las repuestas (Tabla 7), correspondiendo a los mismos EPM que respondieron incorrectamente a la tarea 1a). En ambas es necesario considerar la presencia de datos atípicos que influyen sobre el valor de la media. Un ejemplar de este tipo de respuesta indica: "Prefiero trabajar en capital, porque en promedio los salarios son más altos" (Protocolo DE1-GE-05). Por otro lado, ninguna respuesta fue categorizada como C y 66% de las respuestas a este inciso corresponde a la categoría SR (Tabla 7).
La tarea 3c) (Tabla 3) presentó uno de los mayores porcentajes de respuestas de la categoría SR (71%). El 16% de las respuestas corresponde a la categoría NR y 3% a la categoría NC. Se destaca que no se registran respuestas correctas (C) (Tabla 7). Las dos respuestas de la categoría PC (5%) indican un entorno tecnológico que da cuenta de propiedades de la media aritmética; sin embargo, se confunde la unidad en la que estos datos son medidos. Además, estos EPM no responden al efecto que estas transformaciones producen en la dispersión de los datos originales.
La tarea del inciso 4a) (Tabla 4) obtuvo 66% de respuestas de la categoría SR. Mientras que siete EPM manifestaron no conocer el entorno tecnológico para dar respuesta (13% en la categoría NC) o no recordaron el mismo (5% en la categoría NR). El 5% de las respuestas de este inciso pertenece a la categoría PC (Tabla 7). De los protocolos inferimos que los EPM consideran como medida adecuada el rango intercuartílico, aunque no exhiben una justificación de su elección. Un ejemplar de respuesta de la categoría PC señala que "tengo un muy débil recuerdo de como trabajaba los ejercicios de distribución, calculo que algún gráfico de barras me permitiría ver con facilidad cual es la edad con más frecuencia del cuadro" (Protocolo DE1-GE-05). Esta respuesta da cuenta de la falta de comprensión de la tarea, pues siendo la moda la medida resumen que se propone, no se observa el gráfico de caja.
En relación con las repuestas obtenidas para el inciso 4b) (Tabla 4), 58% de las que se recogieron pertenece a la categoría del tipo SR, 13% a la categoría NC y 11% a la categoría NR (Tabla 7). De los protocolos se desprende y que hay confusión entre valores de la variable y frecuencia de los datos, poniendo en evidencia que el entorno tecnológico es débil. En la única respuesta registrada para la categoría PC (3%), se indica una técnica que carece de justificación. La única respuesta registrada en la categoría C (3%) permite inferir que la técnica para realizar esta tarea se basó en el análisis de la información de la tabla de datos.
En cuanto al inciso 4c) (Tabla 4), 58% de respuestas corresponde a la categoría SR, 13% a la categoría NC, 3% a la categoría C y 8% a la categoría I (Tabla 7). La única respuesta que se recoge para la categoría C hace suponer que el entorno tecnológico contempla la noción de percentil P(0,95). En relación con las respuestas recogidas en correspondencia con la categoría PC (11%), ninguna justifica la técnica empleada. Destacamos que en todos los protocolos relevados, no se registró la realización de cálculos para dar respuesta a los incisos del ítem 4 (Tabla 4).
Para todos los incisos del ítem 5 (Tabla 5), el porcentaje de respuestas de la categoría SR es similar: 58% en el inciso 5a), 53% en 5b) y 5c), 55% en 5d) (Tabla 7).
En el inciso 5a) no se registró ninguna respuesta que se corresponda con la categoría C. Por otro lado, 8% de las respuestas pertenece a la categoría NC e idéntico porcentaje corresponde a la categoría NR. Seis repuestas fueron registradas para la categoría I (16%). El 11% de las respuestas pertenece a la categoría PC (Tabla 7). Este conjunto de repuestas no explicita una justificación del correcto valor de verdad asignado a la afirmación.
En lo que toca a las respuestas registradas para el inciso 5b), 7% pertenece a la categoría C. En ellas se indica el valor de la moda de la variable considerada. La categoría I representa 4% de las respuestas. Un ejemplar de respuesta señala que "La moda es 7, el mayor valor que se repite" (Protocolo DE3-GE-07). Aquí se evidencia la ausencia de un entorno tecnológico adecuado, confundiendo los valores de la variable con sus respectivas frecuencias absolutas.
Para el inciso 5c) se registró una sola repuesta de la categoría C (3%) y una sola respuesta de la categoría I (3%) (Tabla 7). De estas producciones se infiere la ausencia de un entorno tecnológico adecuado que justifique el hacer propuesto, pues se confunde frecuencia relativa con frecuencia relativa acumulada.
Para el inciso 5d), no se registraron respuestas de la categoría C. En tanto que para la categoría PC se registró 11% de respuestas (Tabla 7). En las mismas se considera que un valor atípico es aquel que se presenta con frecuencia pequeña, evidenciando un entorno tecnológico inadecuado. Esto se pone en evidencia en las repuestas "Verdadero, porque se ve con poca frecuencia" (Protocolo DE1-GE-05) y "Verdadero. Solo 1 tienen dos hijos" (Protocolo DE3-GE-03).
Dentro de las respuestas del ítem 6 (Tabla 6) se distingue el elevado porcentaje de respuestas de la categoría SR (71%), y la ausencia de respuestas de las categorías NC, NR e I (Tabla 7). Las siete respuestas registradas para la categoría PC (18%) muestran diferentes tipos de variable a relevarse en un teléfono celular. Se han considerado variables discretas, como cantidad de recargas mensuales; continuas, como duración de llamadas, y categóricas, como modelos del smartphone. Sin embargo, las respuestas de esta categoría no incluyen la forma en que los datos de esas variables pueden ser presentados.
3.1 Respuestas al ítem Observaciones
En relación con el ítem abierto denominado Observaciones, 71% de los EPM indicó algún comentario. Las 27 observaciones fueron categorizadas de la siguiente manera:
La categoría NE representa 41% de las observaciones relevadas. Se destaca que las nociones estadísticas no han sido propuestas a estudiar en la formación docente. En particular,
de los problemas propuestos no pude resolver ninguno ya que no sé nada de la rama de estadística. Hay palabras y consignas que no conozco o no sé cómo resolver, ej.: "moda" "media" "dispersión", etc. Tampoco entiendo los gráficos y cómo analizar las tablas. (Protocolo DE1-GE-06)
Aquí, se especifican nociones fundamentales de estadística que el EPM desconoce. Otro ejemplar de respuesta indica que "mi cursada consto mas de probabilidad. Estadística debimos estudiar solos para el final" (Protocolo DE3-GE-07). Un EPM señala: "No he podido resolver las consignas. Creo que el nivel en el profesorado debería ser mejor" (Protocolo DE2-GP-05). De esta respuesta se infiere que, para este estudiante, resulta ser relevante el estudio de la estadística.
La categoría NR representa 26% de las observaciones. En ellas se señala que la imposibilidad de resolver las tareas del CTE obedece al no recordar las nociones que el mismo contempla, como se indica en el Protocolo DE1-GE-07: "Sinceramente no recuerdo la manera de resolver los problemas presentados, sé de que me está hablando, entiendo el vocabulario, pero no recuerdo los parámetros que se utilizan". Este EPM afirma que las tareas abordan nociones que le son familiares, pero que no tiene el recuerdo de las técnicas requeridas para su resolución. Otro ejemplar de respuesta afirma: "Creo que la materia probabilidad se debería dar varios años ya que aprender muchas cosas con ella en un solo año hace que en los años siguientes te olvides de conceptos importantes" (Protocolo DE1-GE-02). Este EPM justifica el olvido indicando que el cúmulo de las nociones estudiadas en la asignatura Probabilidad y Estadística impide su recuerdo y propone destinar más tiempo al estudio de la estadística.
Por otro lado, cuatro respuestas contienen (33%) observaciones pertenecientes a la categoría NER. Destacamos las observaciones recogidas en el protocolo DE-GP-07: "No recuerdo mucho ya que vimos en muy poco tiempo la parte de estadística y no recuerdo algunas fórmulas y que nos hayan dado así la materia". El EPM manifiesta la reducción temporal en el estudio de la estadística. Esto conduce a la desvalorización tanto de la resolución de las tareas estadísticas como de la necesidad de formación en esta materia de los ciudadanos.
Conclusiones
En este trabajo presentamos resultados del diseño e implementación de un cuestionario de tareas estadísticas que fue aplicado a estudiantes para profesor en matemática que realizan sus carreras en ISFD. El CTE involucró tareas relacionadas con nociones estadísticas que los EPM estudiaron durante su formación. Un bajo porcentaje de estudiantes pudo resolver las tareas de manera exitosa. Estos resultados se relacionan directamente con la falta de estudio de la estadística en las aulas de enseñanza secundaria, dado que resultará problemático proponer la resolución de tareas que los mismos profesores encuentran difíciles (Ortiz de Haro & Font, 2014). En acuerdo con Ortiz de Haro y Font (2014), "estas insuficiencias en la comprensión de los profesores justifican la necesidad de una formación específica para desarrollar los conocimientos especializados y comunes" (p. 215).
Las principales dificultades detectadas en los EPM se encuentran en las tareas que requieren interpretar los resultados en relación con nociones estadísticas. En particular, los EPM enfatizan que no pueden resolverlos porque no recuerdan fórmulas. El hecho de no recordar expresiones formales impide que los EPM interpreten las propuestas del cuestionario. Sin embargo, las tareas del CTE no requieren en general de la aplicación de algoritmos de resolución. Si bien son necesarias técnicas de resolución algorítmicas en el estudio de nociones estadísticas, la interpretación de la información contextualizada presentada en tablas y/o gráficos, así como de los valores de medidas de posición y dispersión, se tornan fundamentales en el hacer estadístico. El diseño de las tareas del CTE priorizó la interpretación y el análisis de la información por sobre el cálculo rutinario, dado que este último se desvanece con el tiempo.
Los resultados obtenidos en el hacer propuesto por los EPM del CTE es ratificado en los comentarios que recogimos en el ítem observaciones. En particular, algunos EPM señalan que las dificultades que tuvieron para resolver son atribuidas a la falta de estudio de nociones estadísticas y a tareas diferentes a las realizadas en su formación docente. Esto último lo interpretamos como la diferencia entre tareas que sólo requieren cálculos mecánicos con datos ficticios, por una parte, e interpretación, comparación o descripción de información contextualizada, por otra. Concluimos que docentes para los que el foco central de su formación en estadística no se coloque en interpretar resultados e integrar nociones de estadística para responder, difícilmente se predispondrán a enseñar este tipo de nociones estadísticas. Esto se corresponde con los resultados obtenidos por Moreno, Cardeñoso y González García (2012), quienes señalan que "es la falta de formación en estos temas, según explican algunos docentes, lo que les impide afrontar su enseñanza en forma idónea" (p. 154). Es necesario un cuestionamiento del modo en que la formación de los profesores de matemática se desarrolla en la actualidad. "La mejora de esta formación del profesorado es un reto para hacer realidad la mejora de la enseñanza de la estadística en las escuelas" (Arteaga et al., 2012, p. 295). El estudio de tareas estadísticas pertenecientes a los géneros, interpretar, describir y comparar deberían estar presentes, reduciendo el estudio de tareas que sólo pertenezcan al género calcular. Estas resultan obsoletas, atendiendo a los actuales desarrollos tecnológicos que simplifican los cálculos. Esto permitiría, en los sistemas actuales de enseñanza, destinar más tiempo a la interpretación de los resultados obtenidos en el contexto de los datos.
Lista de referencias
Aiken, L. (1980). Content Validity and Reliability of Single Items or Questionnaire. Educational and Psychological Measurement, 40, 955-959.
Araneda, A., del Pino, G., Estrella, S., Icaza, G., & San Martín, E. (2011). Recomendaciones para el currículum escolar del eje Datos y Probabilidad. Recuperado de http://www.soche.cl/archivos/Recomendaciones.pdf
Arteaga, P., Batanero, C., Cañadas, G., & Gea, M. M. (2012). Evaluación del conocimiento especializado de la estadística en futuros profesores mediante el análisis de un proyecto estadístico. Educação Matemática Pesquisa, 14(2), 279-297.
Azcárate, P. (1996). Estudio de las concepciones disciplinares de futuros profesores de primaria en torno a las nociones de aleatoriedad y probabilidad. Granada: Comares.
Azcárate, P. (2006). ¿Por qué no nos gusta enseñar estadística y probabilidad? Trabajo presentado en la XII Jornada de Investigación en el Aula de Matemáticas: Estadística y azar, de la Sociedad Andaluza de Educación Matemáticas THALES y el Departamento de Didáctica de la Matemática, Universidad de Granada, Granada Recuperado de http://thales.cica.es/granada/?q=node/4
Azcárate, P., & Cardeñoso, J. M. (2011). La Enseñanza de la Estadística a través de Escenarios: implicación en el desarrollo profesional. Bolema, Boletim de Educação Matemática, 24(40), 789-810.
Batanero, C. (2013). Sentido estadístico: Componentes y desarrollo. En J. M. Contreras, G. R. Cañadas, M. M. Gea & P. Arteaga (Eds.), Actas de las I Jornadas Virtuales en Didáctica de la Estadística, Probabilidad y Combinatoria (pp. 55-61). Granada: Departamento de Didáctica de la Matemática-Universidad de Granada.
Batanero, C., Gea, M. M., López-Martín, M. M., & Arteaga, P. (2017). Análisis de los conceptos asociados a la correlación y regresión en los textos de bachillerato. Didacticae: Revista de Investigación en Didácticas Específicas, 1, 60-76. doi:10.1344/did.2017.1.60-76
Ben-Zvi, D., & Sharett-Amir, Y. (2005). How do Primary School Students Begin to Reason about Distributions? En K. Makar (Ed.), Reasoning About Distribution: A Collection of Current Research Studies [CD-ROM] (pp. 1-27). Brisbane, Australia: University of Queensland.
Bosch, M., Fonseca, C., & Gascón, J. (2004). Incompletitud de las organizaciones matemáticas locales en las instituciones escolares. Recherches en Didactique des Mathématiques, 24(2-3), 205-250.
Cardeñoso, J. M. (2001). Las creencias y conocimientos de los profesores de primaria andaluces obre la matemática escolar. Modelización de concepciones sobre la aleatoriedad y probabilidad (Tesis doctoral inédita). Universidad de Cádiz, España.
Carnel, L. J. (1997). Computers in Probability Education. En R. Kapadia & M. Borovcnik (Eds.), Chance Encounters: probability in education (pp. 169-211). Boston: Kluwer Academic Publishers.
Celina, H., & Campo, A. (2005). Aproximación al uso del coeficiente alfa de Cronbach. Revista Colombiana de Psiquiatría, 34(004), 572-580.
Chevallard, Y. (1999). El análisis de las prácticas docentes en la teoría antropológica de lo didáctico. Recherches en Didactique des Mathématiques, 19(2), 221-266.
Chevallard, Y. (2017). ¿Por qué enseñar matemáticas en secundaria? Una pregunta vital para los tiempos que se avecinan. La Gaceta de la Real Sociedad Matemática Española, 20(1), 159-169.
Cobo, B. (2003). Significado de las medidas de posición central para los estudiantes de secundaria (Tesis doctoral). Recuperada de www.ugr.es/~batanero/pages/ARTICULOS/tesiscobo.pdf
Estepa, A. (2008). Interpretación de los diagramas de dispersión por estudiantes de Bachillerato. Enseñanza de las Ciencias, 26(2), 257-270.
Estrada, A. (2002). Análisis de las actitudes y conocimientos estadísticos elementales en la formación del profesorado (Tesis doctoral inédita). Universidad Autónoma de Barcelona, España.
Estrada, A. (2011). Evaluación de actitudes y conocimientos estadísticos elementales de profesores de educación primaria en formación. En J. J. Ortiz (Ed.), Investigaciones actuales en educación estadística y formación de profesores (pp. 89-102). Granada: Departamento de Didáctica de la Matemática-Universidad de Granada.
Estrada, A., Batanero, C., & Fortuny, J. M. (2004). Un estudio sobre conocimientos de estadística elemental de profesores en formación. Educación Matemática, 16(1), 89-111.
Estrada, A., Batanero, C., & Fortuny, J. M. (2006). Análisis de las actitudes y conocimientos estadísticos elementales en la formación del profesorado. Tarbiya, 38, 79-90.
Fonseca, C. (2004). Discontinuidades matemáticas y didácticas entre la enseñanza secundaria y la enseñanza universitaria (Tesis doctoral). Recuperada de http://www.atd-tad.org/wp-content/uploads/2012/07/TESIS__en__PDF.pdf
Gal, I. (2002). Adult’s statistical literacy: Meaning, components, responsibilities. International Statistical Review, 70(1), 1-25.
Garfield, J. (2002). The Challenge of Developing Statistical Reasoning. Journal of Statistics Education, 10(3).
Garfield, J., & Ben-Zvi, D. (diciembre, 2007). How Students Learn Statistics. Revisited: A Current Review of Research on Teaching and Learning Statistics. International Statistical Review, 75(3), 372-396.
Godino, J. D., Giacomone, B., Batanero, C., & Font, V. (abril, 2017). Enfoque Ontosemiótico de los conocimientos y competencias del profesor de matemáticas. Bolema, 31(57), 90-113.
Hernández, R., Fernández, C., & Baptista, P. (2010). Metodología de la investigación (5ª ed.). México: Mc Graw Hill.
Lucas, C. (2010). Organizaciones matemáticas locales relativamente completas (Memoria de investigación). Universidad de Vigo, España. Recuperado de http://www.atd-tad.org/wp-content/uploads/2012/07/DEA-Catarina-Lucas_versi%C3%B3n-preliminar.pdf
Moore, D. (1990). Uncertainty. En L. Steen (Ed.), On the shoulders of giants: New approaches to numeracy (pp. 95-137). Washington: National Academy Press.
Moreno, A., Cardeñoso, J. M., & González García, F. (2012). Las dificultades detectadas en un grupo de estudiantes del profesorado de educación primaria cuando afrontan la asignación de probabilidades. En M. Marín-Rodíguez & N. Climent (Eds.), Actas del XV Simposio de la Sociedad Española de Investigación en Educación Matemática. Investigación en Educación Matemática (pp. 153-178). Castilla: Sociedad Española de Investigación en Educación Matemática. Recuperado de http://www.seiem.es/docs/comunicaciones/GruposXVSimposio.pdf
Ortiz de Haro, J. J., & Font. V. (2014). Pre-service Teachers’ Common Content Knowledge Regarding the Arithmetic Mean. REDIMAT, Journal of Research in Mathematics Education, 3(3), 192-219.
Pino del, G., & Estrella, S. (2012). Educación estadística: relaciones con la matemática. Pensamiento Educativo. Revista de Investigación Educacional Latinoamericana, 49(1), 53-64.
Serradó, A., Azcárate, P., & Cardeñoso, J. M. (2005). Randomness in textbooks: the influence of deterministic thinking. En M. Bosch (Ed.), IV Conference of the European Society for Research in Mathematics Education (pp. 559-569). Barcelona: Universidad Ramon Llull.
Serradó, A., Azcárate, P., & Cardeñoso, J. M. (2006). Analyzing teacher resistance to teaching probability in compulsory education. En A. Rossman & B. Chance (Eds.), Proceedings of the Seventh International Conference on. Teaching Statistics (pp. 1-20). Salvador: International Association for Statistical Education.
Skate, R. (1999). Investigación con estudio de casos. Madrid: Morata.
Watson, J. M. (2001). Profiling Teachers’ Competence and Confidence to Teach Particular Mathematics Topics: The Case of Chance and Data. Journal for Mathematics Teacher Education, 4(4), 305-337.
Welch, S., & Comer, J. (1988). Quantitative Methods for Public Administration: Techniques and Applications. Indiana: Dorsey Press.
Wild, C. J., & Pfannkuch, M. (1999). Statistical thinking in empirical enquiry (with discussion). International Statistical Review, 67(3), 223-265.